Understanding waveforms
Praat for Beginners
Tutorial: Understanding waveforms
This page deals with the basic features of waveform diagrams
- The waveform diagram
- Sinusoidal waves
- Periodicity
- Amplitude
- Frequency
- Transients
Additional waveform tutorials:
1. The waveform diagram
- Figure 1 illustrates the waveform of the simplest type of sound. Simplest, that is, in the sense that it consists of just one tone, with no other sound mixed in. Theoretically, this is the sound of a tuning fork. It’s not easy to find a natural simple tone. Whistling or some birdcalls are possible examples. But it only needs one other tiny sound component added to it, and it’s no longer a simple tone.
 |
Figure 1. A sine wave, or simple tone.
|
- The vertical scale represents sound pressure, the horizontal scale represents time.
- So the diagram is showing how pressure varies with time. Not just any pressure, but the sound pressure of this particular tone relative to the atmospheric pressure, which is 0 sound pressure.
- The sound pressure rises and falls above and below the atmospheric pressure – alternating between denser and thinner, between compression and rarefaction.
- The sound pressure scale goes from positive to negative to accommodate that alternation. The values of the sound pressure scale (-1 to +1) are arbitrary. This is also what you will see when you look at the waveform of a speech recording in Praat. The standard unit of pressure is Pascal, but the true Pascal values can only be shown for a recording when it has been calibrated for measuring Pascal.
Top
2. Sinusoidal waves
- Now look at the shape of the wave in Fig. 1. This one is sinusoidal, it happens to be exactly the same shape as that of the sine function. This gives a special meaning to simple tone. As soon as the shape of the waveform differs from sinusoidal, it is no longer a simple tone but a complex sound with more than one component. The sine wave is one example of a number of basic waveforms with known properties that are described in the Standard waveforms tutorial.
Top
3. Periodicity
- The wave in Fig. 1 also appears to be repetitive as it alternates between compression and rarefaction. A wave that repeats like this is said to be periodic, and the smallest repeating segment of the wave is the cycle.
- In contrast, the waveform of speech is complex and variable, reflecting the variety of vowels and consonants that are used and the dynamic nature of speech articulation with one or more articulators usually in motion at any time (see examples in the What is coarticulation? section). Figure 2 shows a speech example from Swedish:
 |
Figure 2. The waveform of the Swedish phrase som vi (that we …) spoken by a radio newsreader
|
- Figure 3 shows a few cycles from the vowel sampled at time B in Fig. 2.
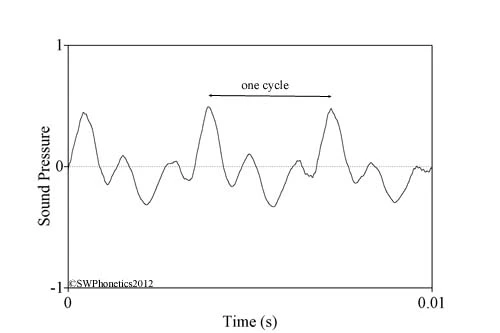 |
Figure 3. The waveform of three cycles from the vowel sampled at time B in Fig. 2
|
- The strict criterion of periodicity is the repetition of identical activy, something that rarely, if ever, happens in speech. Compare these three cycles in Fig. 3. They’re superficially similar but they differ in various details. For practical purposes, this is nevertheless regarded as periodic, loosely if you wish, or quasiperiodic.
- The periodicity of this example comes from the glottal vibrations of the voice. This is a complex waveform (its shape is definitely not sinusoidal), the components being the partial, or harmonic, tones of the voice. It was Jean-Baptiste Fourier (1768-1830) who discovered that any periodic function can be expressed as the sum of sine functions. Fourier analysis (or a fast version, fast Fourier transform or FFT) is still used to resolve complex waveforms into sinusoidal components.
- Before leaving periodicity, Fig. 4 shows an example of a wave that is aperiodic (not periodic)
 |
Figure 4. The waveform of 0.01secs sampled from the consonant [s] at A in Fig. 2
|
- This is the same time span, 0.01secs, as the three cycles seen in Fig. 3. There’s no regularly repeated pattern of activity in Fig. 4, all alternations between compression and rarefaction are random. This is the hissing sound of the consonant [s] in som, and the aperiodic waveform reflects the random character of the turbulent airstream created in the vocal tract for this type of consonant.
Top
4. Amplitude
- The magnitude of the sound pressure alternations, measured from 0, is known as amplitude. For example, the activity at B in Fig. 2 has an amplitude of about 0.6 on this arbitrary scale, while the activity at A has an amplitude of about 0.2. Amplitude corresponds roughly to loudness, or audibility (but only roughly, because hearing is also dependent on tone height; we do not hear very low or very high tonal ranges so well; (more in the next section on frequency).
- The amplitude at C in Fig. 2 is 0, i.e. silent. Brief moments of silence occur during the occlusions of unvoiced stop consonants. But there are no silent gaps between words in everyday speech. But there are regular breathing pauses that might or might not be silent depending on audible respiration.
- Silence in a recording is also relative. A speech recording made in a room with loud ventilation, or busy motor traffic outside, will have a constant background noise that obscures “silent” moments in the speech. That’s why speech recordings intended for analysis are made in as silent conditions as possible, to ensure that you are measuring speech features and not something else.
- The weakest audible sound, if your hearing is perfect, is like the rustling of a single leaf at one metre distance. Don’t bother trying. In the real world, that leaf will be drowned by all the other noises of modern life. And in any case, the wind that makes it rustle will be more audible.
- Note that 1 and -1 on this scale do not represent the maximum or pain threshold of human hearing. It represents the performance limit of the audio equipment used all the way from the person speaking and through your computer. For Fig. 2, that means all the way from the radio studio microphone and amplifiers, through the radio transmitter and my receiver, and into my computer. In practice there are even lower limits. The closer a signal amplitude gets to 1, the more likely it is that some electronic components will introduce distortions. That’s why you’re usually safe when recording to a level around 0.5, but beyond that most recording equipment will start flashing yellow as a warning, and finally red to let you know that disaster has already occurred (see the section on the Praat recording level meters).
- These examples demonstrate that sound pressure amplitude is related to energy. Higher sound pressure means more energy in the sound wave. Increase the sound pressure by 6dB and the energy will be doubled; increase sound pressure by 12dB, and the energy will be quadrupled, and so one. The more energy you have in the sound wave, the more likely you are to damage something.
- The trumpets at Jericho were reputed to have destroyed the city walls. Organs have to be carefully designed to match them to the building where they will be installed, to avoid causing structural damage. There was a time when earphones were so sensitive they were destroyed by a strong electric audio signal before your ears were damaged. Today, earphones are so robust they can survive a signal that is strong enough to damage the ears.
- The ear transforms acoustic energy into nerve impulses at the hair cells of the cochlea. The acoustic energy bends a hair cell, prompting it to emit an impulse. Excessive energy bends hair cells too far, weakening or permanently destroying them. Natural sounds are usually tolerable, at distances from the source that are safe from other injuries (thunderstorms, landslides, volcanic eruptions and so on). Primates in trees should be safe from excessive sound. Hammering sounds (repeated impulses rather than continuous sound) are dangerous, so makers of flint tools must have experienced occupational hearing loss.
- Your first rock concerts or other severe noise exposures might weaken your hearing for hours. Subsequent warning signs include weakened hearing for a day or more, or intermittent tinnitus (a sensation of ringing). Continued exposure leads to permanent tinnitus or hearing loss.
Top
5. Frequency
- Frequency expresses how often something happens – one birthday a year, ten rainy days a month, four London trains an hour, and so on. That is, defined incidents per time unit.
- The frequency of a periodic wave is the number of cycles that occur per second. Look again at the sine wave in Fig. 1. Referring one cycle to the time scale, its duration is 0.01 secs, corresponding to a frequency of 100 cycles per second (100cps or 100Hz). In the real world this corresponds to a tone towards the bottom of the bass singing range, or near the bottom of the adult male speaking range. An octave above this (double the frequency for an octave) is 200Hz, near the top of the adult male speaking range or the lower part of the adult female speaking range. An octave higher again (double the frequency once more) is 400Hz, the middle of a child’s speaking range, and close to the 440Hz of a standard tuning fork. Finally, one more octave above this is 800Hz, near the top of the soprano singing range.
- Now look at Fig. 3 again. The duration of one cycle there is 0.035secs, so the corresponding frequency is 283Hz. This is in the upper part of the speaking range of adult female voices.
- The complex vowel sound of Fig. 3 is composed of a series of tones spaced with an interval equal to the cycle frequency. You cannot see these component tones just by looking at the wave, they have to be calculated. For this example, the cycle frequency happens to be 283Hz, so the series continues with 566, 849, 1132, 1415 … etc. Hz. All these component tones are known as partials, or harmonics. Alternatively, the lowest (first) partial is referred to as the fundamental frequency and the others as overtones.
- We do not hear acoustic activity equally well at all frequencies. The activity we hear best is roughly between 2000Hz and 5000Hz. Telephone communication is usually limited to about 300Hz-3500Hz. Most speech activity occurs between 100Hz and 8000Hz. With absolutely perfect hearing we might hear down to 20Hz and up to 20000Hz. The lowest note on a piano might be around 50Hz .
- Subsonic and infrasound refer to sound vibrations below 20Hz. Ultrasonic and ultrasound refer to sound vibrations above 20000Hz. Supersonic, on the other hand does not refer to frequency but to velocity (faster than the speed of sound, 350m/s or 1235km/h).
Top
6. Transients
- A transient is a sudden and brief burst of acoustic energy, for example a bursting firecracker, the snap when you break a branch, a handclap. Transients occur in speech as the plosive releases of stop consonants.
- Figure 5 is an example of transients in speech, the plosive release of [t].
 |
Figure 5. Waveform of the Swedish word berättat (told) spoken by a newsreader.
|
- Figure 5 has two examples of [t] bursts, shown by the arrows. The transients look like sharp spikes. The fuzzy looking activity following these two transients is aperiodic activity, the aspiration phase that is typical of Swedish unvoiced stops.
Top
©Sidney Wood and SWPhonetics, 1994-2013





